These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems In the case of the triangle, their side's ratios are 1 2 3 \sqrt3 3Right Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles2 n = 2 × 4 = 8 Answer The length of the hypotenuse is 8 inches You can also recognize a triangle by the angles As long as you know that one of the angles in the rightangle triangle is either 30° or 60° then it must be a special right triangle

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Right triangle 30 60 90 calculator
Right triangle 30 60 90 calculator- A triangle is a special type of right triangle that has a 30degree angle and a 60degree angle in addition to the right angle This triangle hasUse this value to label the other two sides of the triangle Use the values on the triangle to




30 60 90 Triangle Explanation Examples
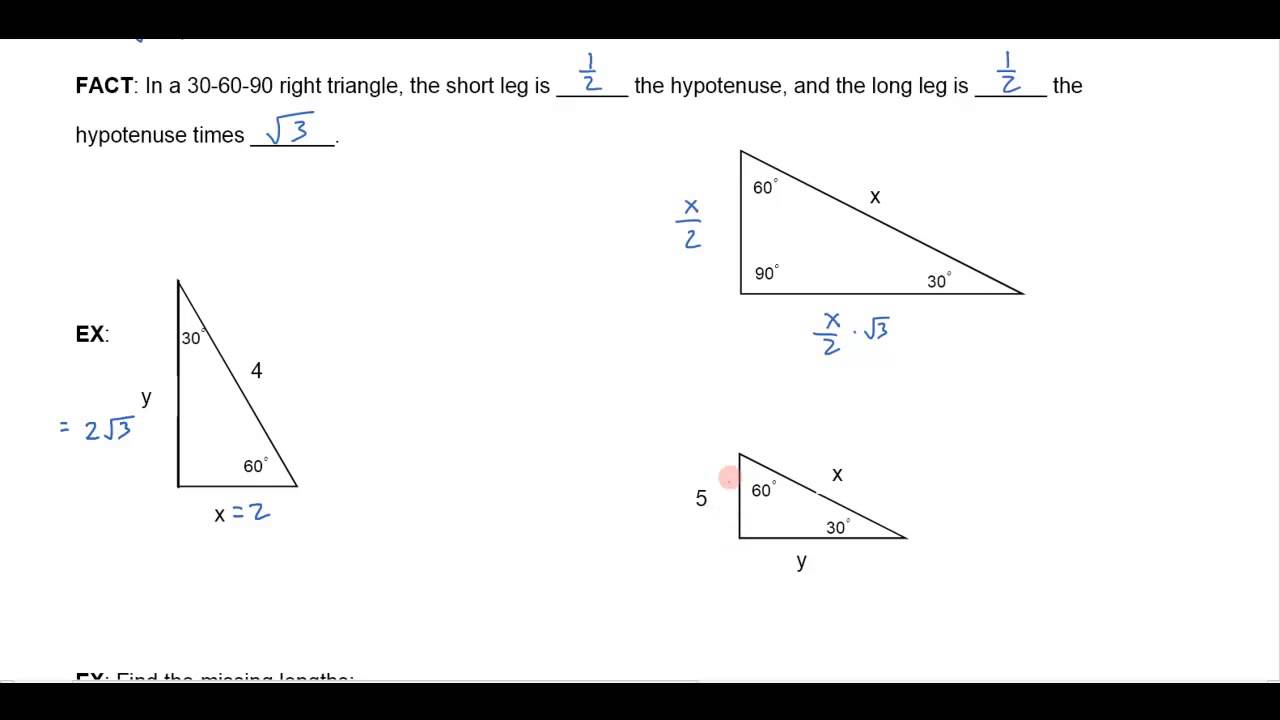
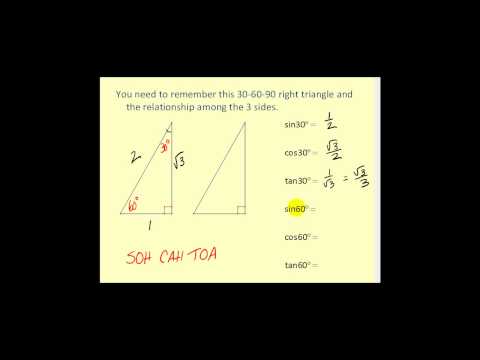
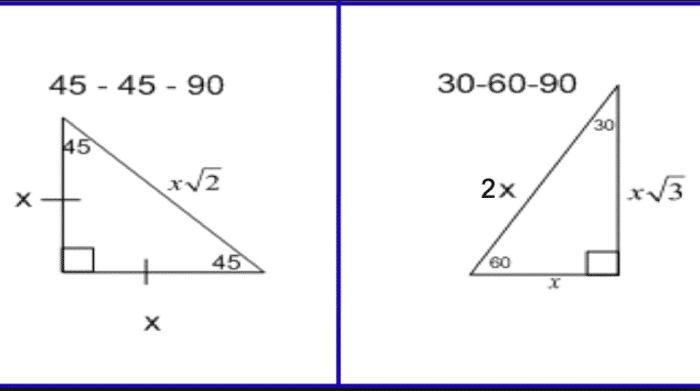
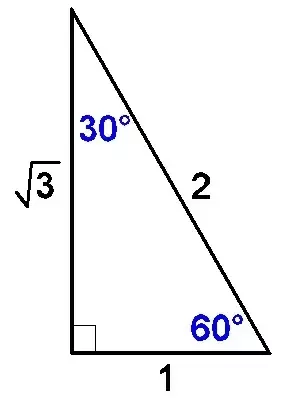
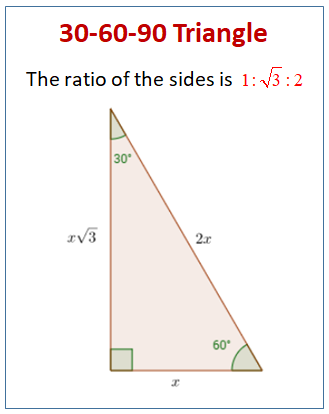
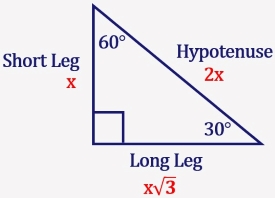
THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that below• area = 05 * long side * short side;A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x , x 3 , and 2 x In a 30 ° − 60 ° − 90 ° triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is 3 times the length of the shorter leg
A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!Check out this tutorial to learn about triangles! A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another
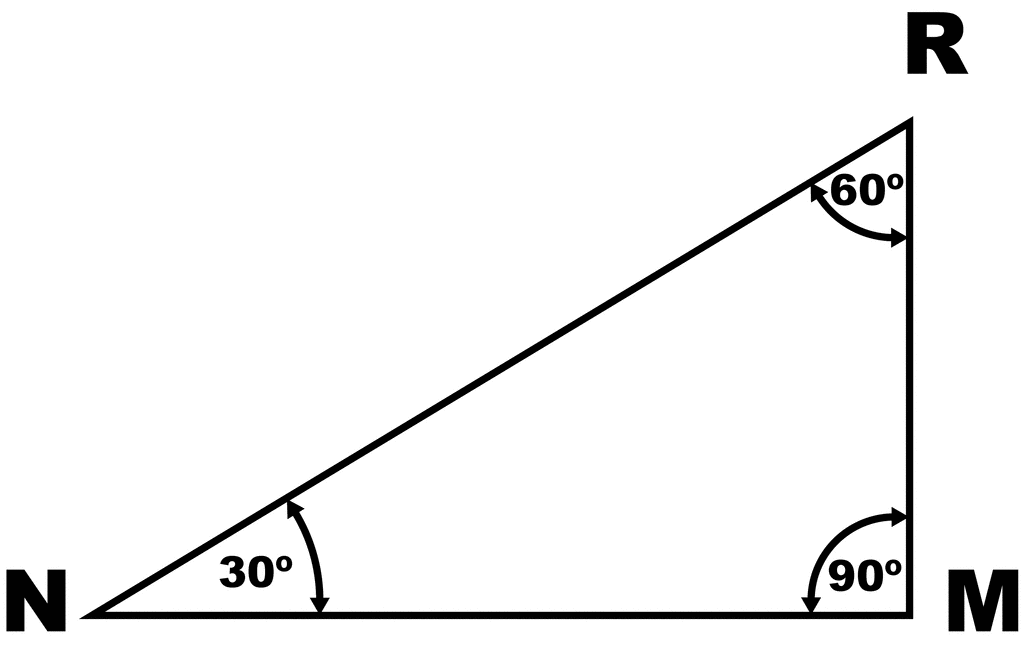
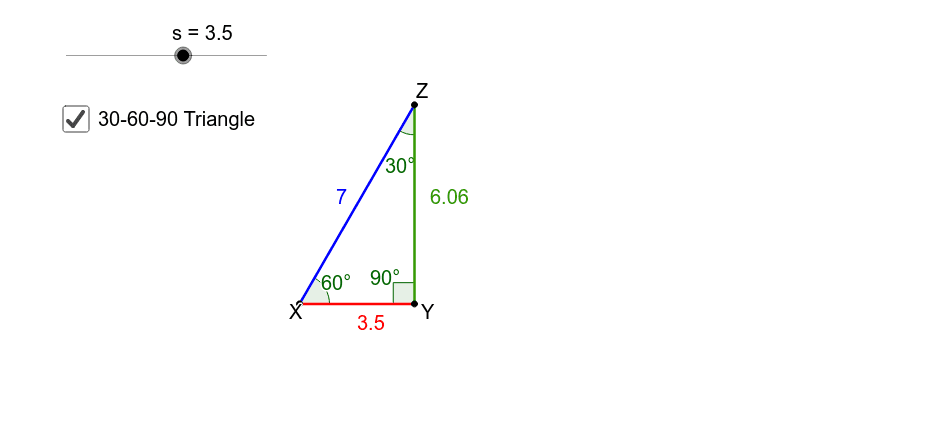
Represents the angle measurements of a right triangle This type of triangle is a scalene right triangle The sides are in the ratio of , with the across from the 30, the as the hypotenuse, and the across from 60 Using variables, it can be written as The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule?A triangle where the angles are 30°, 60°, and 90° Try thisIn the figure below, drag the orange dots on each vertexto reshape the triangle Note how the angles remain the same, and it maintains the same proportions between its sides This is one of the 'standard' right trianglesyou should be able recognize on sight



Trigonometry




The Complete Guide To The 30 60 90 Triangle
• long side = hypotenuse * sin(60̊);What I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is theLearn how to solve for the sides in a Special Right Triangle in this free math video tutorial by Mario's Math Tutoring009 What are the Ratios of t




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



The Easy Guide To The 30 60 90 Triangle
A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√ (3/2) This means that the hypotenuse is twice as long as the shorter leg and the longer leg is the square root ofThe 45 45A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!



Solving A 30 60 90 Right Triangle Youtube




30 60 90 Right Triangles Solutions Examples Videos
Watch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VITriangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functionsIt is a triangle where the angles are always 30, 60 and 90 As one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x




Right Triangle 30 60 90 Problems And Answer Key Tpt




Special Right Triangles Review Article Khan Academy
100 The special right triangle that is formed by drawing the diagonal of a square What is a triangle? Get Your Chances The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SAT A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middle




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangles
Check out this tutorial to learn about triangles!Two of the most common right triangles are and the degree triangles All triangles have sides with the same basic ratio If you look at the 30–60–90degree triangle in radians, it translates to the following The figure illustrates the ratio of the sides for the degree triangle By Rich Zwelling, Apex GMAT Instructor Date 7th January, 21 Right Triangle In a previous piece, we covered the right triangle, also known as the isosceles right triangleThere is another socalled "special right triangle" commonly tested on the GMAT, namely the right triangle Like the isosceles right, its sides always fit a specific ratio,




The 30 60 90 Triangle Topics In Trigonometry



The Easy Guide To The 30 60 90 Triangle
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherAnswer and Explanation 1 To solve a triangle, we want to find the lengths of all of its sides and the measures of all of its angles Since the measures of the angles of aMultiply and simplify cot (60")cos (45") Numerator = Denomirator = On your own paper, draw a 30°60°90° right triangle Label the shortest side a length of 2 (inches);



Special Right Triangles Proof



30 60 90 Right Triangle Clipart Etc
A triangle is a special right triangle The other type of special right triangle is These numbers represent the degree measures of the angles The reason these triangles are considered special is because of the ratios of their sides they are always the same!Trigonometry Examples Popular Problems Trigonometry Solve the Triangle tri {} {30} {} {60} {} {90} Side Angle b = c = a = A = 30 B = 60 C = 90 Side Angle b = c = a = A = 30 B = 60 C = 90 There is not enough information to solve for all of the sides and angles of• hypotenuse = long side * ;




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangles
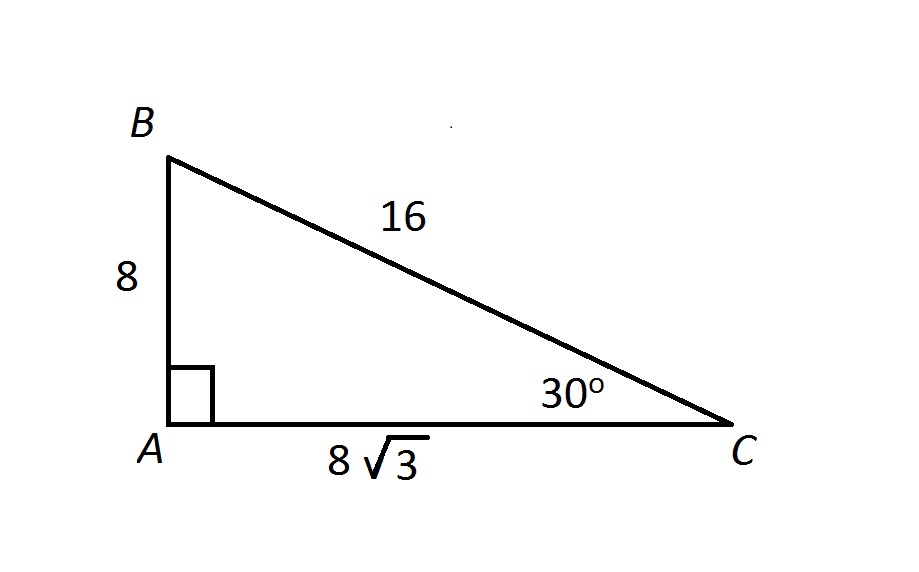
Using the technique in the model above, find the missing side in this 30°60°90° right triangle Short = 5 , hypotenuse = 10 Long = 5 sqrt 3 Using the technique in the model above, find the missing sides in this 30°60°90° right triangle Short = 2 Long = 2 sqrt 3The triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 Here, a right triangle means being any triangle that contains a 90° angle A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1sqrt (3)2 That is to say, the hypotenuse is twice as long as the shorter leg, and



1




How To Work With 30 60 90 Degree Triangles Education Is Around
30 °60 °90 ° Triangles Title PowerPoint Presentation Author Pam Ford Last modified by Cathy Privitt Created Date 1/1/1601 1000 AM Document Right Triangles Hypotenuse equals twice the smallest leg, while the larger leg is sqrt (3) times the smallest % Progress MEMORY METER This indicates how strong in your memory this concept is Practice Preview Assign Practice TL;DR Properties Of A Triangle A right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads)




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Explanation Examples
A triangle is a right triangle with angles 30^@, 60^@, and 90^@ and which has the useful property of having easily calculable side lengths without use of trigonometric functions A triangle is a special right triangle, so named for the measure of its angles Its side lengths may be derived in the following manner Begin with an equilateral triangle of sideHow to use a special right triangle () to solve problems a/c = sin (30°) = 1/2 so c = 2a b/c = sin (60°) = √3/2 so b = c√3/2 = a√3 Also, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given



The Easy Guide To The 30 60 90 Triangle




5 8b 30 60 90 Special Right Triangles Youtube
About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric featuresTriangles 100 A triangle in which all the sides have the same measurement What is an equilateral triangle?A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Ratio Formula Video
100 The name of 9 sided polygon NONAGON?A 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ Formulas of triangle with angle 30̊ 60̊ 90̊ • perimeter = long side short side hypotenuse; Definition of a triangles, including angles and side lengths A 3 0 − 6 0 − 9 0 3 0 − 6 0 − 9 0 is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




Special Right Triangles Fully Explained W 19 Examples
In the study of trigonometry, the triangle is considered a special triangle Knowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60°• long side = hypotenuse * ;Triangles Concept A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three



1 10 30 60 90 Right Triangles K12 Libretexts




30 60 90 Special Right Triangle Calculator Inch Calculator
This page shows to construct (draw) a 30 60 90 degree triangle with compass and straightedge or ruler We are given a line segment to start, which will become the hypotenuse of a right triangle It works by combining two other constructions A 30 degree angle, and a 60 degree angleBecause the interior angles of a triangle always add to 180 degrees, the third angle mustA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and the longer leg is the square root of 3 times




30 60 90 Triangle Theorem Ratio Formula Video



Triangle 30 60 90 Clipart Etc




30 60 90 Triangle Theorem Ratio Formula Video



Special Right Triangles Complete Reference Guide The Education



1




30 60 90 Right Triangle Side Ratios Expii




File 30 60 90 Triangle 2 Svg Wikimedia Commons




30 60 90 Triangle Explanation Examples



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Example Problem Video Khan Academy



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions




30 60 90 Triangle 30 Degree Right Angle Transparent Png 1024x592 Free Download On Nicepng



Special Right Triangles 30 60 90 Geogebra




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Right Triangles Read Geometry Ck 12 Foundation




30 60 90 Triangle Identity Gmat Geometry Apex Gmat Blog
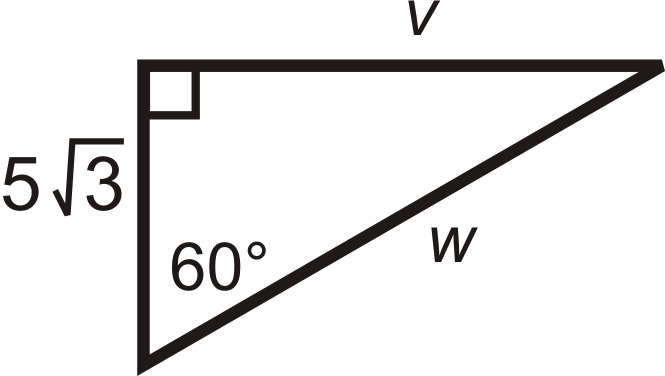



1 10 30 60 90 Right Triangles K12 Libretexts




Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Inter Math Methods Studying Math Physics And Mathematics
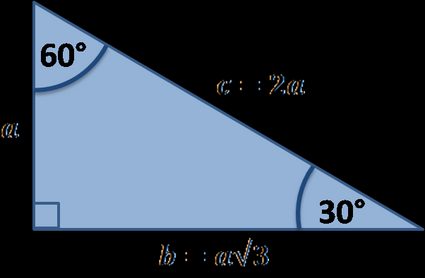



30 60 90 Triangle Calculator Formula Rules



30 60 90 Right Triangles And Algebra Examples Beacon Learning



45 45 90 And 30 60 90 Triangles Zona Land Education




30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books



Is A 3 4 5 Triangle Also A 30 60 90 Triangle Quora




Learn About The 30 60 90 Triangle Caddell Prep Online
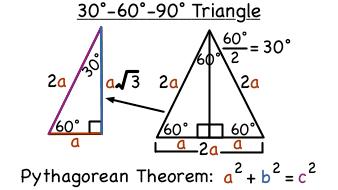



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangle Definition Theorem Formula Examples




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




Special Right Triangles Interactive Notebook Page 30 60 90 Mrseteachesmath Blogspot Co Trigonometry Worksheets Triangle Worksheet Math Interactive Notebook




5 30 60 90 Triangles Geometry15a




30 60 90 Triangle Calculator Formula Rules



Special Right Triangles Proof
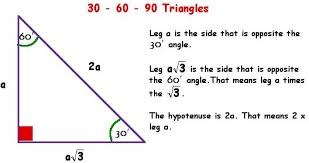



30 60 90 Right Triangle Theorem By Stephanie Joaquin Infographic



Special Right Triangle 30 60 90 Mathondemand Com



30 60 90 Right Triangles Math Trigonometry Trig Triangles Right Triangles Showme




30 60 90 Right Triangles Read Geometry Ck 12 Foundation



Solve A 30 60 90 Triangle With Gradea



Solution I Dont Know How Do 30 60 90 Triangles That Already Have One Side And Also 45 45 90 Triangles And Sin 1 And All That Please Help



Special Right Triangles 30 60 90 Math Geometry Triangles Right Triangles Showme



1




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Right Triangles Free Math Help




30 60 90 Right Triangles Ck 12 Foundation



Special Triangles Hiset Math



30 60 90 Triangle Rules




30 60 90 Right Triangles Consider The Following




How To Use The Special Right Triangle 30 60 90 Studypug




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
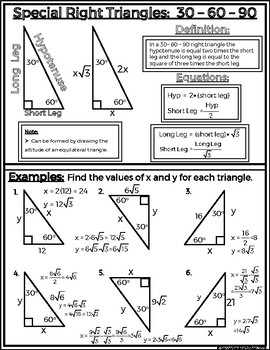



Special Right Triangles 45 45 30 60 90 Notes Sheet Graphic Organizers




A Quick Guide To The 30 60 90 Degree Triangle Dummies
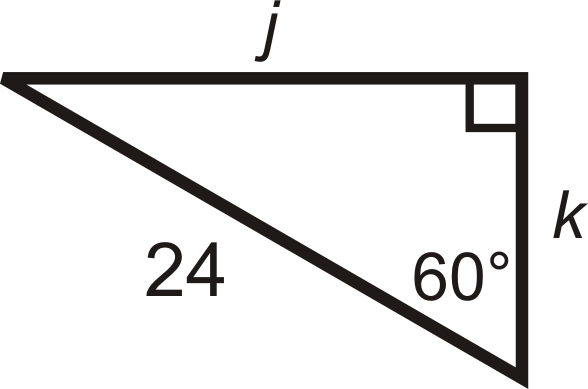



30 60 90 Right Triangles Read Geometry Ck 12 Foundation




30 60 90 Triangles Spock S Guide To Math 4
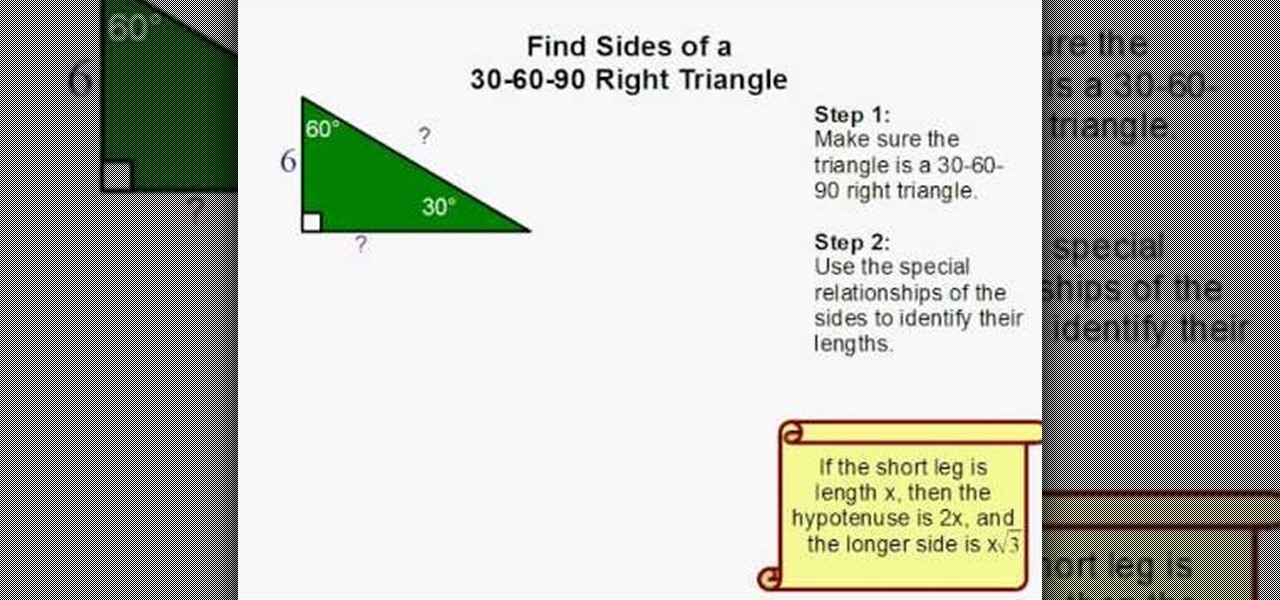



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto
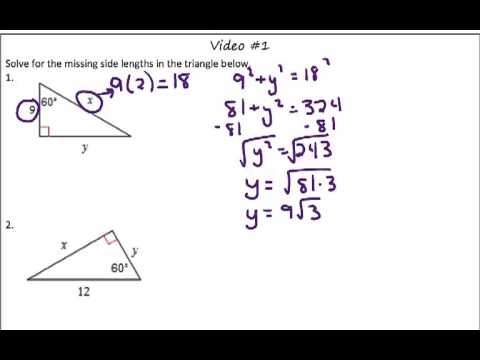



Special Right Triangles 30 60 90 Video 1 Youtube




A Quick Guide To The 30 60 90 Degree Triangle Dummies
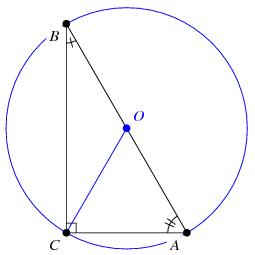



30 60 90 Triangle From Wolfram Mathworld



45 45 90 Special Right Triangle Ppt Download
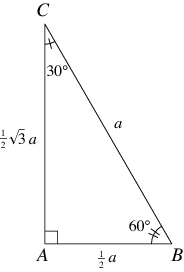



30 60 90 Triangle From Wolfram Mathworld




Test Prep Thursday Special Right Triangles Mathnasium
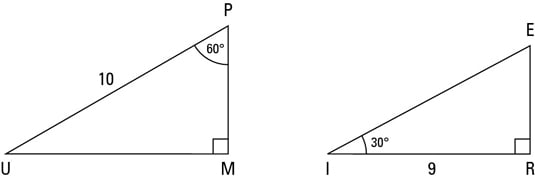



Identifying The 30 60 90 Degree Triangle Dummies
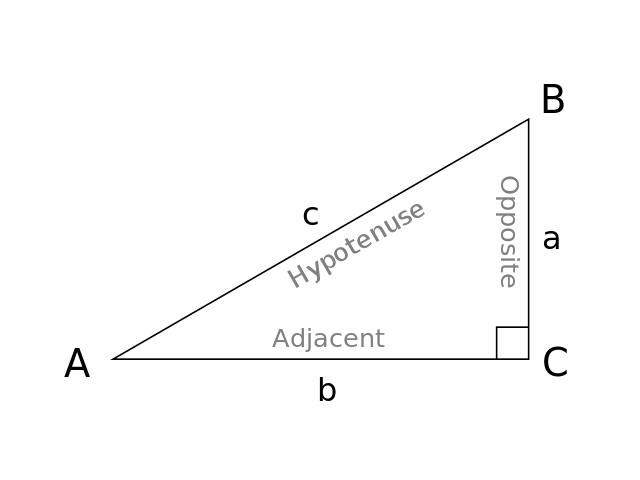



30 60 90 Triangle Formulas Rules And Sides Science Trends



Math Figure 30 60 90 Triangle




30 60 90 Triangle



5 5 22 Special Right Triangles 30 60 90 Mosley Nc Math 2 Honors S2
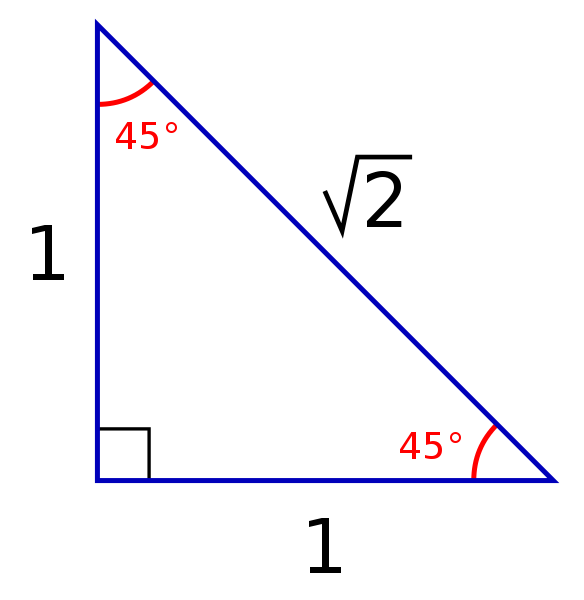



30 60 90 Triangle Formulas Rules And Sides Science Trends




The 30 60 90 Triangle Topics In Trigonometry
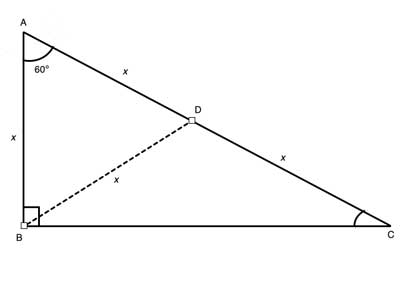



30 60 90 Triangle Geometry Help




Ppt 30 60 90 Right Triangles Powerpoint Presentation Free Download Id



Right Triangle Degrees 30 60 90 Clipart Etc




Special Right Triangles
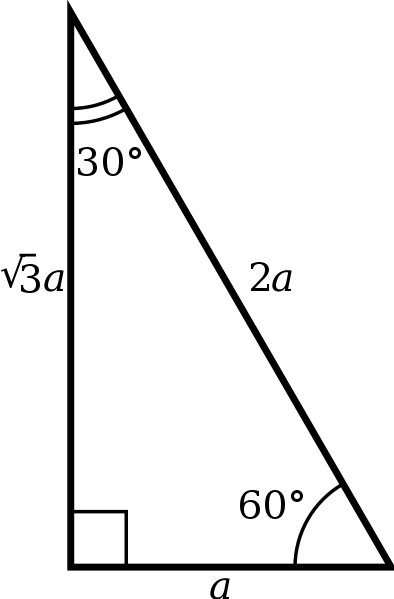



30 60 90 Triangle Formulas Rules And Sides Science Trends




The Complete Guide To The 30 60 90 Triangle
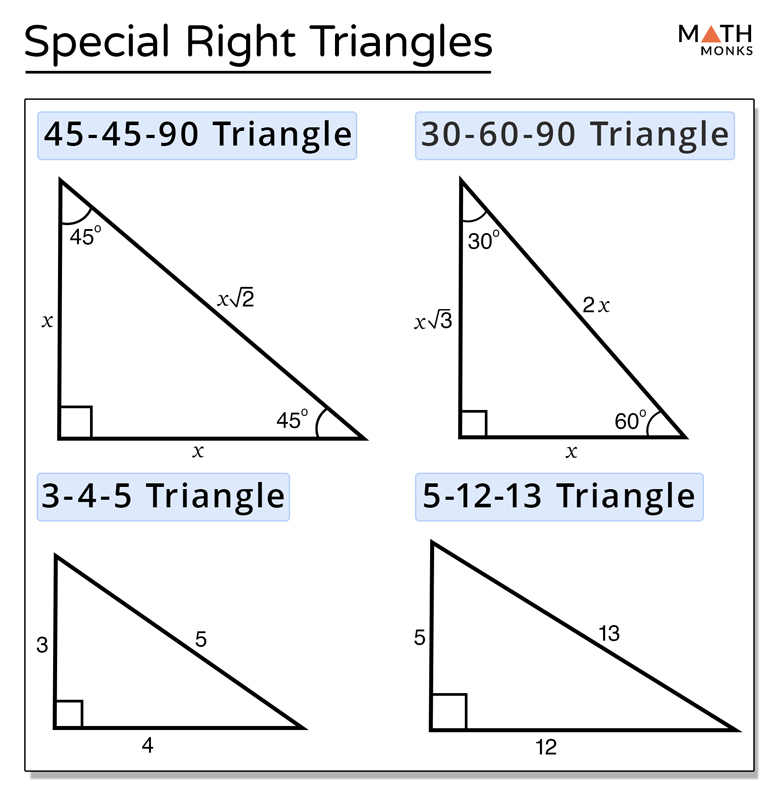



Special Right Triangles Definition Formula Examples



3



0 件のコメント:
コメントを投稿